2015年中级工商管理预习知识(第一章考点十)_第2页

X1≥0,X2≥0
(4)找出使目标函数达到最优的可行解,即为该线性规划的最优解用图解法求解，见下图：

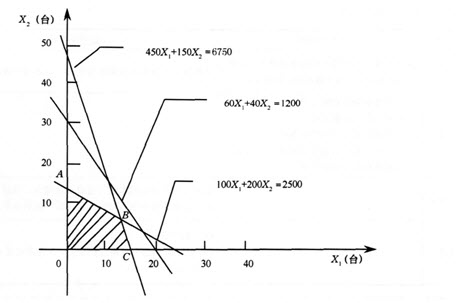
分别以X1、X2为横纵坐标，将约束方程绘制于表中，由于有三个约束方程，因此有三条直线。三条直线共同构成的区域(阴影部分)为可行解的区域。目标函数的最大值一定在由约束方程构成的可行解区域的凸点上。通过计算三个凸点A(0，12．5)、B(13，6)、C(15，0)为所对应的目标函数值，则满足使目标函数最大值的点为B点。即当生产A产品l3台、8产品6台时企业获得的利润最大，为50×13+90×6=1190(元)。
【提示】如何把约束条件画在坐标中?
以60X1+40X2≤1200为例：
直线60X1+40X2=1200
当X1=0，则40X2=1200，X2=30，即该直线与纵轴交于(0，30)点。
当X2=0，则60X1=1200，X1=20，即该直线与横轴交于(20，O)点。
在坐标中找到这两点，连线即可得到直线60X1+40X2=1200。约束条件要求的是≤1200，所以符合条件的是直线60X1+40X2=1200左下方的,且X1≥0，X2≥0的区域。
【例36·单选题】某企业生产某产品的固定成本为45万元，单位可变成本为l5元，产品单位售价为20元，其盈亏平衡点的产量为（　　）件。
A．12857
B．22500
C．30000
D．90000
【答案】D
【解析】本题考查确定型决策方法中的盈亏平衡点法。盈亏平衡点的产量=固定成本／(单位售价一单位可变成本)=450000／(20-15)=90000(件)。
(二)风险型决策方法

方法	期望损益决策法	决策树分析法
含义	通过计算各个方案的期望损益值①，并以此为依据，选择收益最大或损失最小的方案作为最佳评价方案	将构成决策方案的有关因素，以树状图形的方式表现出来,并据以分析和选择决策方案的一种系统分析法

续表

方法	期望损益决策法	决策树分析法
步骤	(1)确定决策目标 (2)预测市场状态,估计发生的概率 (3)拟订可行方案 (4)计算收益值或损失值 (5)计算各可行方案的期望损益值 (6)比较各方案的期望损益值，选择最优可行方案	下面结合例题讲解
适用范围		特别适于分析比较复杂的问题
构成		决策结点“口”、方案枝、状态结点“o”和概率枝

注：①期望损益值等于该方案在各种可能市场状态下的损益值与其对应的概率的乘积之和。
【例37·单选题】某厂在下一年拟生产某种产品。需要确定产品批量。根据预测估计。这种产品市场状况的概率是：畅销为0．4．一般为0．5．滞销为0．1。产品生产采取四种批量的生产方案如下，根据期望